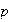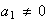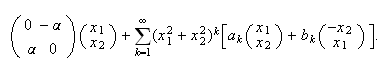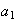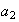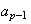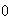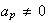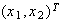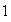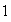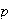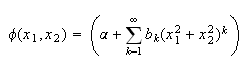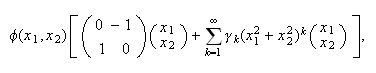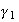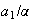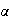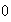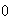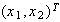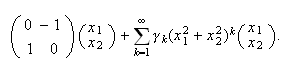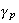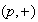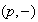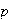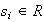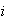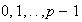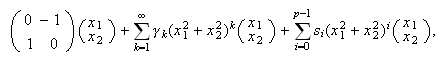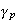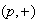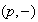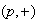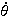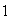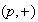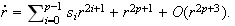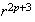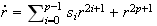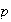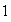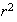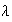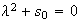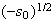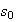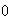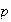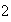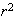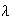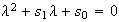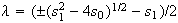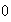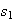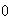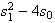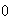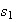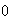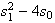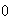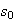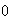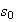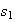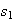Cusp and Generalized Hopf bifurcations
Here the bifurcations concern singularities with co-dimension greater than 1.
These are only unfolded by local families that depend on more than 1
parameter.
Cusp bifurcation
Given
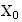 a smooth vector field with a cusp singularity at the
origin. Then
a smooth vector field with a cusp singularity at the
origin. Then
 but
but
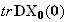 =
= =
=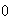 and
and
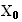 has normal form (with
has normal form (with
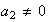 and
and
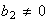 ).
).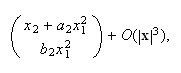 The
local
family
The
local
family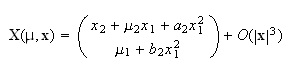 is
a versal unfolding of the cusp singularity above. (Note that the cusp
singularity requires at least two parameters to completely unfold it).
Considering this local family
is
a versal unfolding of the cusp singularity above. (Note that the cusp
singularity requires at least two parameters to completely unfold it).
Considering this local family
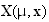 ,
under some conditions (not shown here) in particular about parameters, it is
possible to generate three bifurcation types: (1) Saddle
node, (2) Hopf bifurcation, (3)
Saddle connection.
,
under some conditions (not shown here) in particular about parameters, it is
possible to generate three bifurcation types: (1) Saddle
node, (2) Hopf bifurcation, (3)
Saddle connection.
Generalized Hopf bifurcations
Generalized Hopf bifurcations. (Takens 1973b, Guckenheimer
& Holmes 1983, Arrowsmith & Place 1990). Here, we describe the
generalized Hopf singularity of type
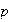 .
The vector field in the previous co-dimension 1 Hopf bifurcation was obtained
by posing
.
The vector field in the previous co-dimension 1 Hopf bifurcation was obtained
by posing
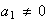 in the normal
form
in the normal
form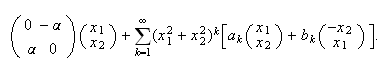 If
a degeneracy is introduced by posing
If
a degeneracy is introduced by posing
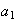 =
=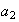 =
= =
=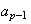 =
=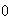 with
with
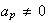 ,
then the system above is said to have a generalized Hopf
singularity of type
,
then the system above is said to have a generalized Hopf
singularity of type
 at
at
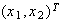 =
= .
(Note that a co-dimension
.
(Note that a co-dimension
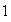 Hopf singularity is said to be of type
Hopf singularity is said to be of type
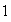 ).
The framework of the generalized Hopf singularity highlights
the relationship between the degeneracy of a singularity and the number of
parameters contained in its versal unfolding.
).
The framework of the generalized Hopf singularity highlights
the relationship between the degeneracy of a singularity and the number of
parameters contained in its versal unfolding.
If a Hopf singularity of type
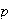 occurs, it is possible to reduce the system above to a simpler system.
Given
occurs, it is possible to reduce the system above to a simpler system.
Given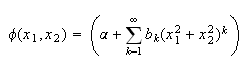 that
can also be
written:
that
can also be
written: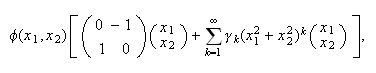 with
with
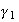 =
=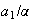 .
Because
.
Because
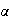 >
>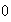 ,
we have
,
we have
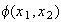 >
>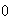 for all
for all
 enough close to the origin. Thus there exists a neighborhood of
enough close to the origin. Thus there exists a neighborhood of
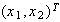 =
= on which the system is topologically equivalent to the (simpler)
vector
field:
on which the system is topologically equivalent to the (simpler)
vector
field: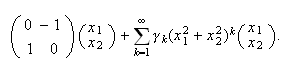 While
preserving the topological equivalence, we can replace
While
preserving the topological equivalence, we can replace
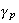 by
by
 in the vector field above. Two cases are then possible according to a
singularity of the type:
in the vector field above. Two cases are then possible according to a
singularity of the type:
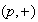 or
or
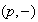 .
A versal unfolding for the vector field above can be obtained through the
following Takens theorem (1973b):
.
A versal unfolding for the vector field above can be obtained through the
following Takens theorem (1973b):
According to the sign of
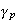 ,
the unfoldings of in this theorem gives two cases
,
the unfoldings of in this theorem gives two cases
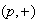 and
and
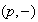 .
Here, we only describe the first case
.
Here, we only describe the first case
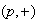 ,
and the latter case can be related to the other by a time reversal (so the
stabilities of fixed points and limit cycles are inverted). The formula in
this theorem, through the polar form
(
,
and the latter case can be related to the other by a time reversal (so the
stabilities of fixed points and limit cycles are inverted). The formula in
this theorem, through the polar form
( with here
with here
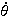 =
=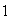 ),
gives for
),
gives for
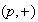 the bifurcational behavior by using the equivalent equation:
the bifurcational behavior by using the equivalent equation:
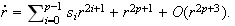 The behavior is independent of the terms of order
The behavior is independent of the terms of order
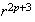 (as described for the co-dimension 1 Hopf bifurcation), so it suffices to
consider
(as described for the co-dimension 1 Hopf bifurcation), so it suffices to
consider
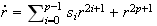 .
This equation in particular provides limit cycles. (1) For
.
This equation in particular provides limit cycles. (1) For
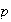 =
=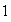 ,
by posing
,
by posing
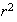 =
=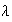 ,
we obtain
,
we obtain
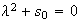 ,
then a limit cycle occurs whose radius is
,
then a limit cycle occurs whose radius is
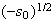 only when
only when
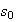 <
<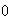 .
(2) For
.
(2) For
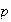 =
=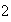 ,
by posing
,
by posing
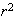 =
=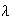 ,
we obtain
,
we obtain
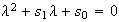 and non-trivial zeros result from
and non-trivial zeros result from
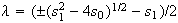 .
Then we obtain:
.
Then we obtain:
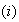 If
If
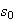 >
>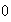 and
and
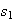 >
>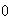 (or
(or
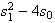 <
<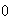 ):
no limit cycle but a repelling spiral.
):
no limit cycle but a repelling spiral.
 If
If
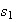 <
<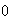 and
and
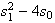 >
>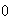 :
two limit cycles.
:
two limit cycles.
 If
If
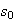 <
<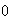 :
one limit cycle. (see
Fig.
:
one limit cycle. (see
Fig. below).
below). This
figure shows the bifurcation diagram for the type-(2,+) Hopf bifurcation. It
shows that a supercritical (subcritical) Hopf bifurcation occurs when
This
figure shows the bifurcation diagram for the type-(2,+) Hopf bifurcation. It
shows that a supercritical (subcritical) Hopf bifurcation occurs when
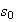 increases through zero with
increases through zero with
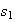 <
< (subcritical with
(subcritical with
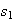 >
>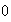 ),
and a double limit cycle bifurcation occurs on the semi-parabola. If
),
and a double limit cycle bifurcation occurs on the semi-parabola. If
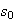 decreases through the semi-parabola, a non-hyperbolic limit cycle occurs and
then divides into two hyperbolic cycles.
decreases through the semi-parabola, a non-hyperbolic limit cycle occurs and
then divides into two hyperbolic cycles.
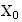 a smooth vector field with a cusp singularity at the
origin. Then
a smooth vector field with a cusp singularity at the
origin. Then
 but
but
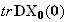 =
= =
=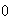 and
and
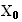 has normal form (with
has normal form (with
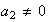 and
and
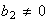 ).
).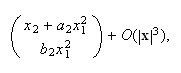 The
local
family
The
local
family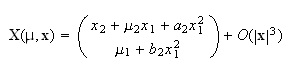 is
a versal unfolding of the cusp singularity above. (Note that the cusp
singularity requires at least two parameters to completely unfold it).
Considering this local family
is
a versal unfolding of the cusp singularity above. (Note that the cusp
singularity requires at least two parameters to completely unfold it).
Considering this local family
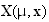 ,
under some conditions (not shown here) in particular about parameters, it is
possible to generate three bifurcation types: (1) Saddle
node, (2) Hopf bifurcation, (3)
Saddle connection.
,
under some conditions (not shown here) in particular about parameters, it is
possible to generate three bifurcation types: (1) Saddle
node, (2) Hopf bifurcation, (3)
Saddle connection.