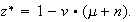Goodwin Model (1967)
A few words about the model. Consider that the production function has
complementary factors according to the following
equation: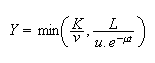 we
know that such an assumption is useful to engender fluctuations. The effective
labor at the period
we
know that such an assumption is useful to engender fluctuations. The effective
labor at the period
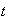 is denoted
is denoted
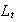 but the working population is
but the working population is
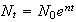 so that the labor rate is
so that the labor rate is
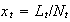 .
The wage depends on the labor rate according to an assumption of the Philips
curve type. The profits are entirely reinvested, they are equal to the savings
.
The wage depends on the labor rate according to an assumption of the Philips
curve type. The profits are entirely reinvested, they are equal to the savings
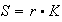 and the part of profits in the global income is the complement of the part of
wages
and the part of profits in the global income is the complement of the part of
wages
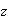 so that
so that
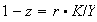 .
The labor depends on the capital according to
.
The labor depends on the capital according to
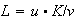 .
Then we have the
system
.
Then we have the
system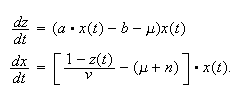 There
is stationary state if
There
is stationary state if
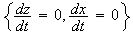 , i.e.,
, i.e.,
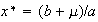 and
and
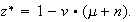
*
[1] ref. to Alain Goergen. "Dynamique Economique. Solutions de problèmes
avec Maple et Matlab". Economica. 2006.
[2] ref. to Gilbert Abraham-Frois.
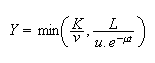 we
know that such an assumption is useful to engender fluctuations. The effective
labor at the period
we
know that such an assumption is useful to engender fluctuations. The effective
labor at the period
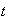 is denoted
is denoted
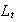 but the working population is
but the working population is
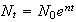 so that the labor rate is
so that the labor rate is
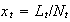 .
The wage depends on the labor rate according to an assumption of the Philips
curve type. The profits are entirely reinvested, they are equal to the savings
.
The wage depends on the labor rate according to an assumption of the Philips
curve type. The profits are entirely reinvested, they are equal to the savings
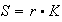 and the part of profits in the global income is the complement of the part of
wages
and the part of profits in the global income is the complement of the part of
wages
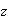 so that
so that
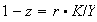 .
The labor depends on the capital according to
.
The labor depends on the capital according to
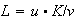 .
Then we have the
system
.
Then we have the
system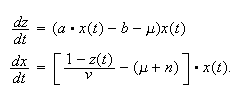 There
is stationary state if
There
is stationary state if
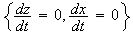 , i.e.,
, i.e.,
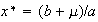 and
and