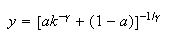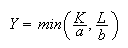
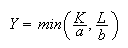
(isoquant
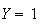 ).
).
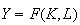 ,
,
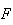 continuous and twice derivable,
continuous and twice derivable,
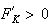 ,
,
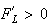 ,
,
and the Inada conditions:
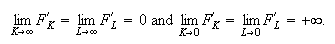
The differential of the production function
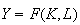 :
:
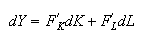
along an isoquant
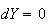 and the Marginal Rate of Substitution (MRS) of
Capital to Labor can be
defined by
and the Marginal Rate of Substitution (MRS) of
Capital to Labor can be
defined by
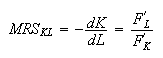
Elasticity of the substitution of Capital to Labor:
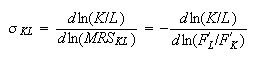
Hypothesis of the remuneration of factors to their marginal productivity,
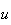 nominal cost of capital,
nominal cost of capital,
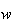 nominal rate of wage,
nominal rate of wage,
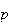 level of prices
level of prices
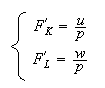
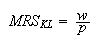
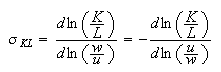
. Constant if
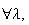
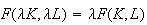
. Decreasing if
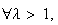
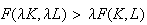
. Increasing if
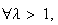
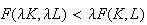
Constant Returns to Scale
Euler theorem:
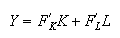
that means
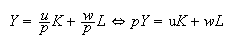
Product Exhaustion Theorem
Zero-Profit
Reasoning per capita:
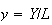 per capita product (or mean productivity of labor)
per capita product (or mean productivity of labor)
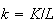 per capita capital
per capita capital
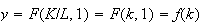
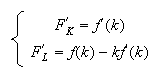
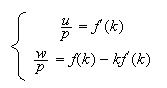
Frontier of the prices of factors
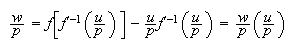
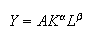
with
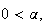
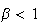
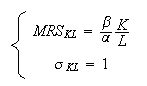
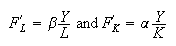
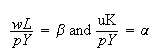
If
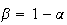 ,
constant returns to scale. Then
,
constant returns to scale. Then
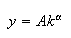
and frontier of the prices of factors:
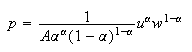
Function of Constant Elasticity of Substitution (CES)
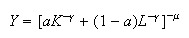
with
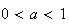 ,
,
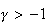 ,
,
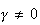
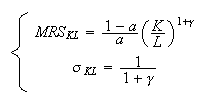
Constant returns to scale if
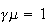 ,
increasing if
,
increasing if
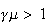 ,
decreasing if
,
decreasing if
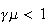 .
.
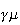 is the scale elasticity. The per capita formulation of
the CES function with constant returns to
scale:
is the scale elasticity. The per capita formulation of
the CES function with constant returns to
scale: