A Few Examples of Pictures (Using MATLAB or c++):
Below, two ex. depicting for the linchirp signal the Atomic Decomposition into Wave Packets by Matching Pursuit:
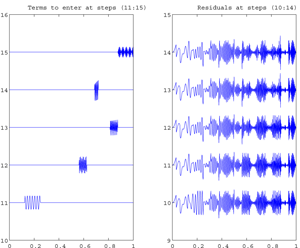
Fig. Example of animation of an Atomic Decomposition into Cosine Packets by Matching Pursuit of the signal Linchirp
, 512 data.
Observe the various shapes of cosine on the left-side of the picture, and the successive residual signals shown on the right-side.
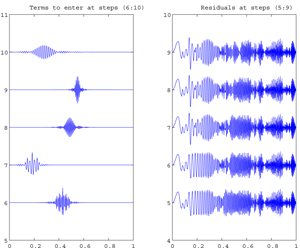
Fig. Example of animation of an Atomic Decomposition into Wavelet Packets by Matching Pursuit of the signal Linchirp
, 512 data.
Observe the various shapes of wavelet on the left-side of the picture, and the successive residual signals shown on the right-side.
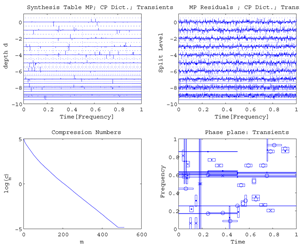
Fig. For the signal transients
and the Matching Pursuit, the figure above displays: 1. Cosine Packet Synthesis Table; 2. Cosine Packet Residuals Table 3. Compression Numbers; 4 Phase plane.
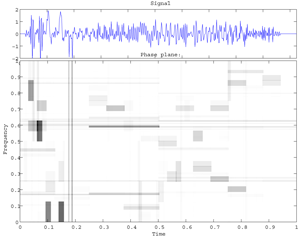
Fig. Image of Time-Frequency Plane, with shading showing Heisenberg cells. Image time-frequency content of atom list for Cosine Packets resulting from Matching Pursuit for the transients
signal , 512 data. In connection with the lower-right picture of the previous Fig.
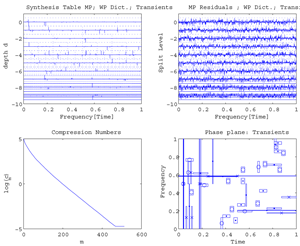
Fig. For the signal transients
and the Matching Pursuit, the figure above displays: 1. Wavelet Packet Synthesis Table; 2. Wavelet Packet Residuals Table 3. Compression Numbers; 4 Phase plane.
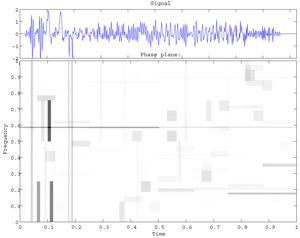
Fig. Image of Time-Frequency Plane, with shading showing Heisenberg cells. Image time-frequency content of atom list for Wavelet Packets resulting from Matching Pursuit for the transients
signal , 512 data. In connection with the lower-right picture of the previous Fig.
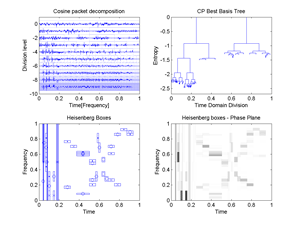
Fig.41 Best Basis for the signal "transients": 1.Cosine packet decomposition, 2.Cosine packet Best Basis Tree, 3.Plot of CP Heisenberg Boxes in the Phase plane, 4.Image of CP Heisenberg Boxes in the Time-Frequency plane.
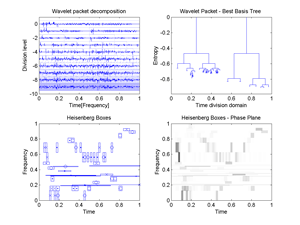
Fig.42 Best Basis for the signal "transients": 1.Wavelet packet decomposition, 2.Wavelet packet Best Basis Tree, 3.Plot of WP Heisenberg Boxes in the Phase plane, 4.Image of WP Heisenberg Boxes in the Time-Frequency plane.
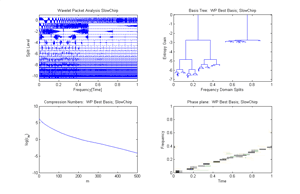
Fig.43 Example of Best basis and WP decomposition of the signal "slow shirp": 1.Wavelet packet decomposition, 2.Wavelet packet Best Basis Tree, 3.Compression Numbers, 4.Image of WP best basis Heisenberg Boxes in the Phase plane.
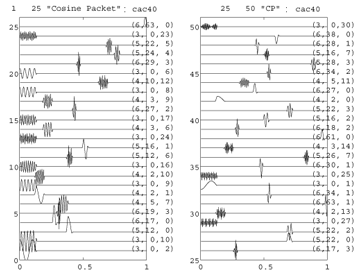
Fig.44 Example of 50 cosine packets repertories for a stock-index.
Fig.45 Detail of the cosine packet repertories above.
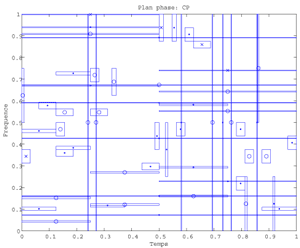
Fig.46 Heisenberg Boxes of Matching Pursuit Fourier Atoms in the Time-Frequency plane for a stock-index sample (512 data).
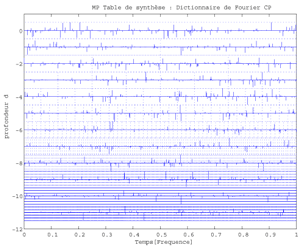
Fig.47 Fourier Dictionary for a longer stock-index sample (x-axis:Time-Frequency; y-axis: Depth of the dictionary).
